
A few details need to be nailed down before we can set up the Deep Cut scene. Some, such as the width of the cut, should be recorded somewhere in the historical record. Other details, like the size of the rock piles, can be calculated.
I’m still looking for a source on the dimensions of the cut. In the meantime we can start on the rock piles.
How tall were they? Contemporary sources describe them as “huge,” achieving heights of up to 50 feet.
Perhaps, but let’s see what a little math tells us.
When it comes to excavating stone, there are two important numbers: angle of repose and swell factor.
Angle of repose is the slope at which a pile of stone (or any material) remains stable. At a greater angle, gravity will overcome friction and the material will slide down the slope. For dolomite and broken rock, the angle of repose varies between 35 to 40 degrees. For now I will use the minimum angle of 35 degrees.
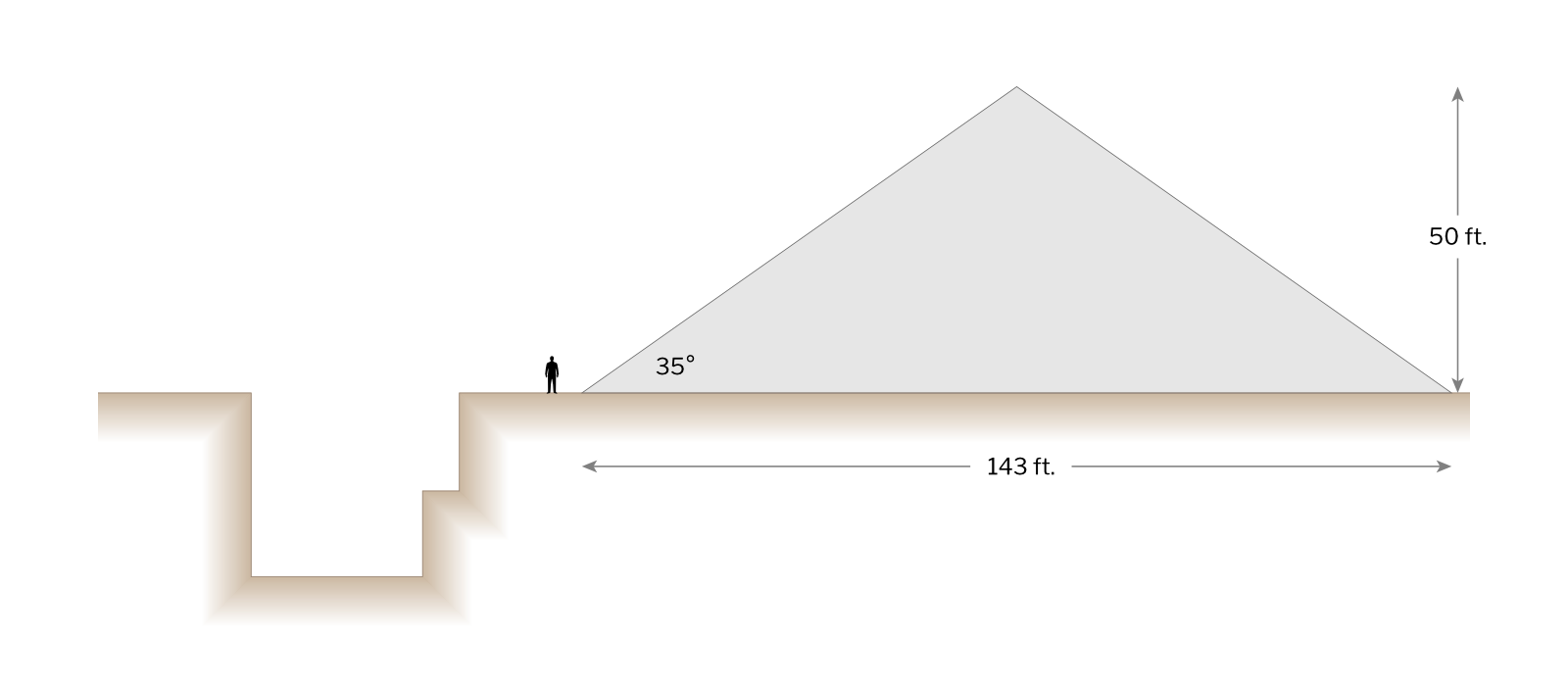
This makes it simple to calculate the size of a cone of broken stone 50 feet high. A 35-degree angle of repose yields a base diameter of about 143 feet.
As the tiny human figure standing next to the cone shows, this is a very large pile of rocks. Much too large based on the size of the canal cut shown in the adjacent profile. In fact, a cone this size would contain more than five times the amount of rubble that would be excavated from the cut. The crane needed to build this pile would also have to be a huge – at least 55 feet tall with a jib of about 90 feet.
Let’s approach the problem properly by starting with the volume of rock to be excavated. For this we need the second important number: swell factor.
Swell factor is the increase in volume that occurs when you break up solid material into smaller, irregular pieces. For dolomite, the factors that I’ve found vary between 50 and 67 percent, with a median of 66. We’ll use the median, which means that every 100 cubic feet of solid dolomite excavated yields 166 cubic feet of broken stone that must be piled up somewhere.
We don’t know the width of the cut yet, so for now I’ll assume a base width of 28 feet plus a 6-foot recess in one wall for the towpath. The maximum depth – which we do know – was 31.5 feet.
The cranes were placed between 60 and 70 feet apart along both sides of the canal. This means, on average, each crane handled a 32.5-foot-long section (the average distance of 65 feet divided by 2). Taking the swell factor into account, this means 50,766 cubic feet of broken stone would be lifted out of the cut by each crane.

This results in a more reasonable-looking pile. The cone would be about 29 feet high and 82 feet in diameter. This represents the maximum pile size at the deepest part of the cut. Elsewhere, the piles would be relatively smaller.
Of course, the rubble pile would not be a cone. The crane would distribute the rubble in an arc described by the tip of the jib. This would reduce the height and width somewhat, depending on the size of the arc and the length of the jib.

The math gets a little dicier now, but an equation can be plugged into Excel to test different volumes and slopes. Then functions can be used to generate the basic shape in Terragen.

After adding a few random displacements, the shape is covered with thousands of rocks. The result is shown at the top of this post. Many variations can be made and placed in the scene.
It may not be 50 feet tall, but it’s still an impressive pile of rocks.

